Most people use "first bet insurance" promos all wrong. They bet a point spread at -110 since it seems safe, or a huge favorite to "lock in" profits.
But there are two mathematically optimal ways to use bonus bets — "convert" them to cash, or bet at plus-money to optimize the expected value.
FanDuel offers this type of promo through the no sweat first bet it sometimes runs as a welcome offer. bet365 has a first bet safety net. Caesars Sportsbook advertises it as "get your first bet back." All these promos function more or less the same.
I'll break down both below. You can still lose your entire deposit with Method 2, so you have to have some risk tolerance or willingness to gamble. But over a large sample, it's how you'll make the most money.
Method 1: Conversion
If you employ a technique called "conversion," you'll profit about 40-50% of the offered insurance value.
Here's how it works.
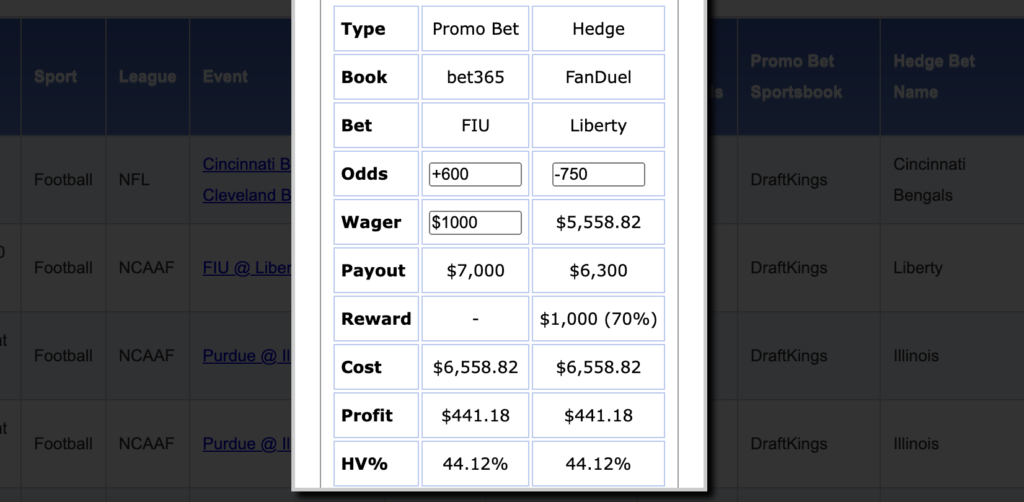
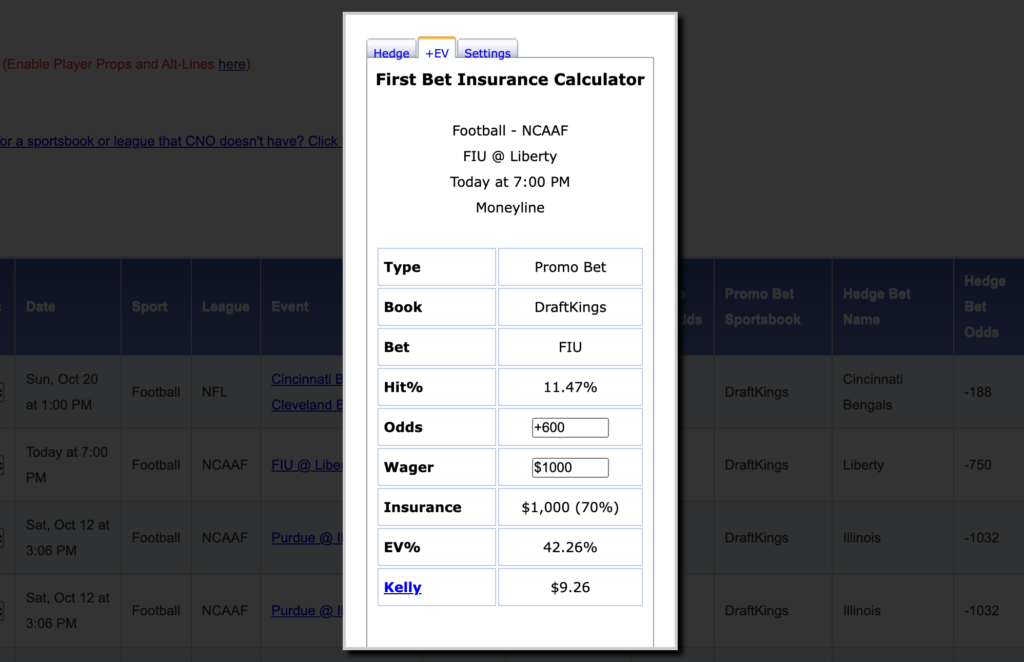
Step 1: Bet a big underdog with your first bet insurance — let's say for this example, it's a $1,000 insurance on your first bet. In the example below, I took FIU +600 against Liberty.
Step 2: Bet the other side of the game at another sportsbook. If your promo bet wins, you're done and you've profited $441. If it loses, move onto Step 3.
Step 3 (if necessary): If the promo bet (underdog) loses you'll get $1,000 in bonus bets back. You'll need to convert those to cash. You can read our full guide to bonus bet conversion here.
No matter who wins, as you can see below from the tools at CrazyNinjaOdds, you'll be up $441 in profit. Just be sure to bet something that cannot end in a push/tie.
Here are a few other tips.
- There are tools like CrazyNinjaOdds that can find these high-converting opportunities for you, so you're not digging through every sportsbook to find the best two lines.
- Stick with main markets like moneylines in major sports (and avoid the NFL, since those games can end in a tie). If you try to wager $5,558 on one side of a random prop, your bet might be rejected.
- Never bet both sides at the same sportsbook, as they'll likely void your promo. They do not like this practice.
- Make sure you have these bets queued up at the same time and place them within seconds of each other, so the lines don't move on you.
Method 2: Betting at Plus-Money
Like with bonus bets, your expected value on first bet insurance/safety net offers is always going to be higher if you bet on longshots. It's a little counter-intuitive in that you want to find a bet that more often triggers the insurance payout, even though you'd obviously prefer to just win your first bet. You don't want to lose, but given that your upside is massive if you do hit and you get the insurance bonus bets if it doesn't hit, it makes mathematical sense to bet something between +300 and +700.
You can also use the CrazyNinjaOdds tools to find bets with high expected value with your first bet safety net.
Here's the expected value calculation:
Scenario 1: You bet a big favorite with your $1,000 insurance at -500 that has an 85% chance to win. Most of the time, you'll win $200. Sometimes, you'll lose $800 if you employ the same strategy on your ensuing bonus bets. A few times, you'll lose the entire $1,000 if your ensuing bonus bet wager also loses.
Your expected value from the $1,000 insurance bet is low — about $45.
The math: .85 * ($200) + .21.85 * (-$800) + .15.15 * (-$1000) = $45
Scenario 2: You bet a big underdog with your $1,000 first bet insurance at +500 that has a 15% chance to win, so 15% of the time you'll win $5,000. Sometimes, you'll lose the entire $1,000. Other times, you'll win $4,000 if you employ a similar strategy with a longshot on your ensuing bonus bet wager.
The math: .15 * ($5000) + .85 * .15 * ($4000) + .85*.85 * (-$1000) = $537
Here, your expected value is much higher — north of $500 cash off the $1,000 wager.
Unfortunately, in today's sports betting environment, there aren't dozens of $1,000 insurance offers and you could lose all $1,000 doing this. So if you're not comfortable losing this much money, consider a different method, even if this is mathematically optimal over a large sample.