A lot of the commentary behind picking a Flex Play vs. Power Play on PrizePicks is quite anecdotal.
"I always lose my three-leg Power Plays by one leg, so take the three-leg Flex Play."
But this misses the big picture — what are the most cost-effective PrizePicks game types, and which ones should you actually be playing?
To determine this, we'll need to convert the total payout into a breakeven percentage, which is the rate at which you'd need to win each individual leg in the long run to breakeven. The breakeven point is high — higher than what it requires you break even betting point spreads in traditional sports betting.
The Math Behind Flex Play vs. Power Play
PrizePicks includes the stake of your entry, so if PrizePicks says you're getting 10x, you're really only profiting 9x, since whatever you entered will come back to you. So it may be easier to use decimal odds, since they work the same way.
We'll detail the math below, but here's the simple summary — the 6-leg and 5-leg Flex Plays actually require you to win legs at the lowest rate to break even, just over 54%. That's inclusive of you getting some money for going 3/5 or 4/5.
The three-leg Flex is the worst, at almost 60% breakeven.
Power Play
There are two steps to calculating the breakeven percentage for a power play (where you need to win every leg) — determine the odds of each leg, then convert that to a breakeven percentage.
1. To determine the "odds" of each leg, you want to find the odds at which two equal legs multiplied together will equal your payout. So for a 3x payout, I just used a simple square root calculator to find that 1.73 is that number.
Converting those decimal odds to American odds, it comes out to about -136.6.
2. To determine the breakeven percentage, you can use our odds calculator or we outlined the math here. The calculation from American odds will vary slightly depending on whether or not your side is the favorite or underdog. Converting -136.6 to breakeven percentage, you get about 57.74% — that's how often you need to be winning each leg to break even with a two-leg Power Play.
Flex Play
The math is a bit more complicated because you have to combine all possibilities of a Flex Play, instead of just a Power Play, which is binary (you either win all legs and win, or lose at least one and lose).
Here's the formula example for a 5-leg flex play:
For each probability of picking correctly (p), we calculate:
5/5 correct: (p⁵) × 10
4/5 correct: (5C4)(p⁴)(1-p) × 2
3/5 correct: (5C3)(p³)(1-p)² × 0.4
2/5 or less: Rest of probability × 0
Then we add these together for expected value. Break-even is when expected value equals 1.0.
5/5: (0.578⁵ × 10) = 0.0621 × 10 = 0.621
4/5: (5 × 0.578⁴ × 0.422 × 2) = 0.2645 × 2 = 0.529
3/5: (10 × 0.578³ × 0.422² × 0.4) = 0.3754 × 0.4 = 0.150
Add that all together = 1.000
Is There a Psychological Element to It?
Perhaps the psychological element is why PrizePicks does it this way. Hitting 6/6 on a flex play — to get the real 25x prize most users are after — is really hard. Assuming all your picks have a 50% chance of winning and you made one lineup per day, you'd expect to have a 6/6 day about once every two months. If you could pick at 55%, you'd expect to go 6/6 about once every 35 days.
This infrequency will lead most users to "playing it safe" and creating smaller lineups, even if the math is even more stacked against you on the smaller legs. If you lose a 6/6 flex play 25 days in a row, will you really go back again the next day?
What About Demons & Goblins?
PrizePicks has made a few key changes to its pricing over the years:
- The introduction of demons (harder to win legs that pay more) and goblins (easier to win legs that pay less)
- Correlation pricing, meaning that if you include two legs where one is more likely to happen if the other one happens, you'll get a worse price.
The pricing engines on the backend at DFS sites like PrizePicks are hidden — if you take two goblins, it doesn't show you the price of each one. But the underlying math on the payouts of the Flex Play vs. Power Play should be the same as above, and each individual leg will be "priced" different.
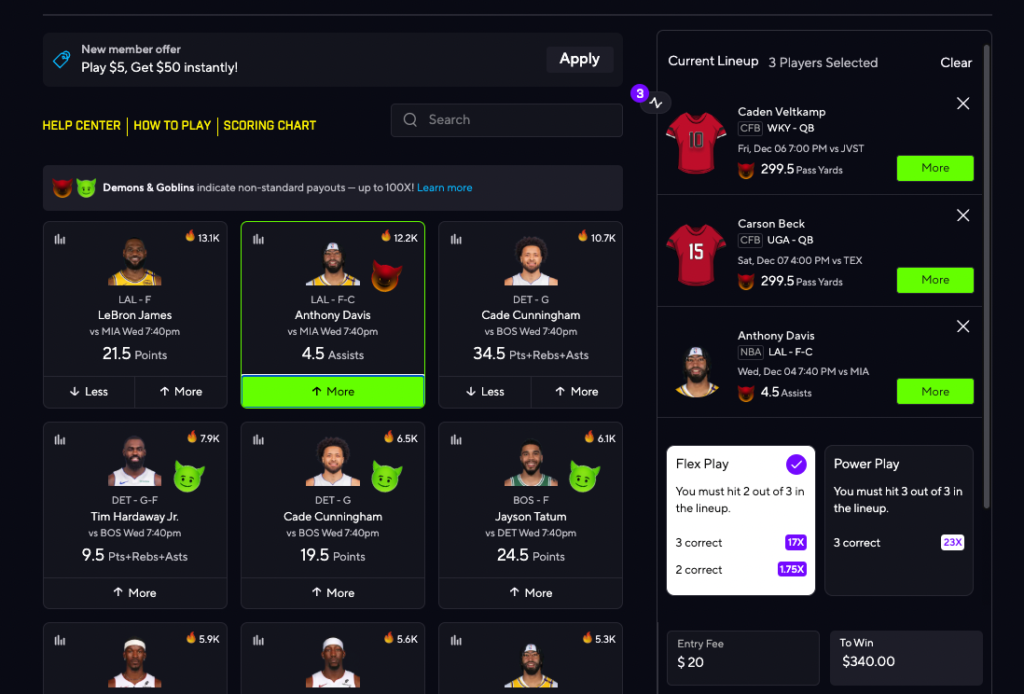
Say you have three demon legs (meaning the payouts are higher) — Anthony Davis more than 4.5 assists, Carson Beck more than 299.5 passing yards and Caden Veltkamp more than 299.5 passing yards — all spitting out different prices when you use just two of the legs. That means each individual leg is different. You can reverse engineer it to find the true price of each leg.
- Veltkamp & Beck = 8x payout
- Veltkamp & Davis = 6x payout
- Davis & Beck = 10x payout
Let v = Veltkamp odds, b = Beck odds, d = Davis odds. The house is for a 3-leg
v × b = 8 × 1.7352941 = 13.88
v × d = 6 × 1.7352941 = 10.41
d × b = 10 × 1.7352941 = 17.35
- Veltkamp: 3.286 decimal odds (+228 American)
- Beck: 4.224 (+322)
- Davis: 3.168 (+216)
There's much more you can do to true to reverse engineer these prices in more complex lineups, but for now, we'll leave it here.